Contrainte qualifiée
Contraintes en
Optimisation sous contraintes mixtes d'égalité et d'inégalité permettant de trouver des situations génériques permettant de remonter de la situation tangente à la situation générale
- elles doivent respecter l'une des conditions suivantes :
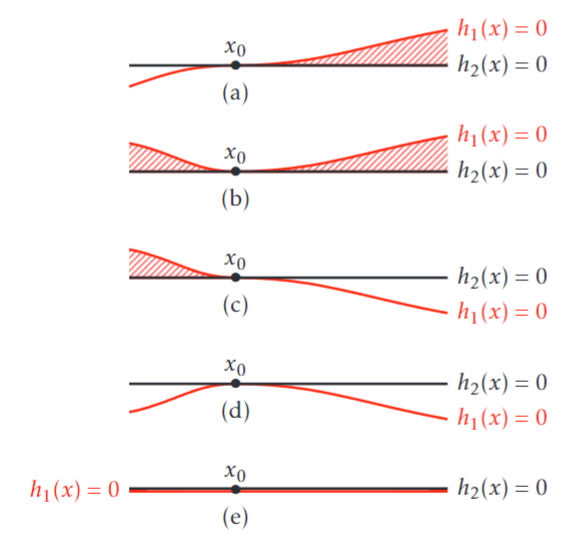
- (il existe une direction qui rentre strictement dans le domaine des contraintes) : \(\exists d\in \ker dg(x_*)\) tq pour toute Contrainte active \(h_j\), \(dh_j(x_*)(d)\lt 0\)Pasted image 20250211111716.png|250
(si \(g\) est affine, on peut faire un peu mieux) : \(g\) est affine et \(\exists d\in\ker dg(x_*)\) tq $$\forall j\in A(x),\begin{cases} dh_j(x_*)\leqslant 0&\text{si}\quad h_j\text{ est affine}\\ dh_j(x_*)\lt 0&\text{sinon.}&\end{cases}$$
(si tout est affine, alors c'est ok) : \(g\) et \(h\) sont affines
- les contraintes qui ne respectent pas ces conditions peuvent générer des situations ambiguës